Second in the Expected Value Series

Welcome back to the second in a series of posts from our good friend Craig Hilsenrath at Option Workbench. In the first Craig introduced us to the concept of Expected Value and why it is important to options trading. With this post that is taken one step further to give us some of the math behind it all and help us to think like the house in a Vegas casino to always put the odds in our favor. We here at Tradier believe the more you know the better off you are. Enjoy the read and stay tuned for the next installment.

Expected Value
In plain language the expected value is the best estimate of a value at some time in the
future. The estimate is calculated by computing the weighted average sum of a set of
possible values. Ideally we’d like to use all possible values to calculate the expected
value but that is not always possible. In general the weighted average is calculated by:

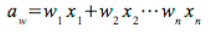
In a simple average the weight associated with each value is 1 divided by the total
number of values, or n in the formula above. For the expected value calculation the
weight for each value is the probability of that value occurring.
The probability associated with a particular value, xi, is found by taking the ratio of the
number of times the xi can occur divided by the total number of observations. A simple
example of this type of calculation is the roll of a single die. The probability of rolling any
of the numbers on the die is 1 out of 6 or 16 2/3 percent.

To make this a little more interesting, suppose a game was constructed where the
operator would roll a fair die and payout 3:1 on a bet to someone who picked the
number that comes up on the die. If a person bets $25 the operator would give them
back $100, their $25 bet plus $75. At first glance this might seem like a good way for the
operator to lose $75. But applying the expected value calculation reveals a different
story. The probability of the operator having to pay out $75 is 1/6 and the probability of
them keeping the $25 is 5/6. So the expected value of this game is:

-75 x 1/6 + 25 x 5/6 = 8 1/3

So on average the operator would expect to make approximately $8.33 per $25 bet. It
should be noted that the operator cannot make $8.33 on any single roll. This illustrates
that the expected value need not be one of the possible outcomes.
To drive this point home consider the expected value of a roulette wheel from the
perspective of the house. A roulette wheel has slots numbered 1 to 36, half of which are
colored black and the other half red. There are two additional slots numbered 0 and 00
colored green for a total of 38 slots. There are two main types of bets that can be made
at a roulette wheel. In the first type of bet the gambler picks a number from 1 to 36 and
if that number comes up the gambler gets paid 35 times the amount bet. In the second
type of bet the gambler picks a color, black or red, and if the color comes up the
gambler receives a 2:1 payout. So if $1 is wagered on red and the ball lands in a red
slot the bettor gets back $2. The expected value of these bets for the house are:

Bet 1: -35 x 1/38 + 1 x 37/38 = 0.0526
Bet 2: -1 x 18/38 + 1 x 20/38 = 0.0526

From the above, the casino expects to make 5.26 cents for every dollar bet at a roulette
wheel. Conversely, a gambler should expect to lose 5.26 cents for every dollar bet at a
roulette wheel.

Using expected value does not guarantee that ANY roll of a die or spin of a roulette
wheel will have a positive outcome for the game’s operator. It does indicate what the
AVERAGE outcome will be over many such rolls and spins and gives the house an
edge over time - essentially the expected profit for the house. Considering the billions of
dollars in annual revenue generated by the gaming industry, expectations do not need
to be very high if many games with positive expectation can be played. This is all very
interesting for casino operators and traveling dice games, but how does it pertain to
trading options?

Coming next week Expected Value in your options strategies. See you then!